使用不同公式的绘图位置¶
计算绘图位置¶
绘制百分位图、分位数图或概率图时,必须计算有序数据的绘图位置。
对于样本\(X\),总体大小为\(n\),第\(j^\mathrm{th}\)个元素的绘图位置定义为
\[\frac{x_{j} - \alpha}{n + 1 - \alpha - \beta }\]
在此方程中,α和β可以取多个值。常见值描述如下:
- “类型 4” (α=0, β=1)
- 经验CDF的线性插值。
- “类型 5” 或 “Hazen” (α=0.5, β=0.5)
- 分段线性插值。
- “类型 6” 或 “Weibull” (α=0, β=0)
- 威布尔绘图位置。所有分布的无偏超额概率。推荐用于水文应用。
- “类型 7” (α=1, β=1)
- R 中的默认值。不推荐用于概率刻度,因为最小值和最大值数据点分别获得0和1的绘图位置,因此无法显示。
- “类型 8” (α=1/3, β=1/3)
- 近似中位数无偏。
- “类型 9” 或 “Blom” (α=0.375, β=0.375)
- 如果数据呈正态分布,则近似无偏位置。
- “中位数” (α=0.3175, β=0.3175)
- 所有分布的中位数超额概率(用于
scipy.stats.probplot)。- “APL” 或 “PWM” (α=0.35, β=0.35)
- 与概率加权矩一起使用。
- “Cunnane” (α=0.4, β=0.4)
- 正态分布数据的近似无偏分位数。这是默认值。
- “Gringorten” (α=0.44, β=0.44)
- 用于古姆布尔分布。
本教程的目的是展示所选的 α 和 β 如何改变概率图的形状。
首先,让我们做一些分析设置...
%matplotlib inline
import warnings
warnings.simplefilter('ignore')
import numpy
from matplotlib import pyplot
from scipy import stats
import seaborn
clear_bkgd = {'axes.facecolor':'none', 'figure.facecolor':'none'}
seaborn.set(style='ticks', context='talk', color_codes=True, rc=clear_bkgd)
import probscale
def format_axes(ax1, ax2):
""" Sets axes labels and grids """
for ax in (ax1, ax2):
if ax is not None:
ax.set_ylim(bottom=1, top=99)
ax.set_xlabel('Values of Data')
seaborn.despine(ax=ax)
ax.yaxis.grid(True)
ax1.legend(loc='upper left', numpoints=1, frameon=False)
ax1.set_ylabel('Normal Probability Scale')
if ax2 is not None:
ax2.set_ylabel('Weibull Probability Scale')
正态与威布尔刻度以及Cunnane与威布尔绘图位置¶
在这里,我们将生成一些假的、正态分布的数据,并从 scipy 定义一个威布尔分布用于概率刻度。
numpy.random.seed(0) # reproducible
data = numpy.random.normal(loc=5, scale=1.25, size=37)
# simple weibull distribution
weibull = stats.weibull_min(2)
现在让我们在威布尔和正态概率刻度上创建概率图。此外,我们将为每个图计算两种不同但常用的绘图位置。
首先,用蓝色圆圈表示数据,并使用威布尔(α=0, β=0)绘图位置。威布尔绘图位置常用于水文学和水资源工程等领域。
用绿色方块表示数据,并使用Cunnane(α=0.4, β=0.4)绘图位置。Cunnane绘图位置适用于正态分布数据,并且是默认值。
w_opts = {'label': 'Weibull (α=0, β=0)', 'marker': 'o', 'markeredgecolor': 'b'}
c_opts = {'label': 'Cunnane (α=0.4, β=0.4)', 'marker': 's', 'markeredgecolor': 'g'}
common_opts = {
'markerfacecolor': 'none',
'markeredgewidth': 1.25,
'linestyle': 'none'
}
fig, (ax1, ax2) = pyplot.subplots(figsize=(10, 8), ncols=2, sharex=True, sharey=False)
for dist, ax in zip([None, weibull], [ax1, ax2]):
for opts, postype in zip([w_opts, c_opts,], ['weibull', 'cunnane']):
probscale.probplot(data, ax=ax, dist=dist, probax='y',
scatter_kws={**opts, **common_opts},
pp_kws={'postype': postype})
format_axes(ax1, ax2)
fig.tight_layout()
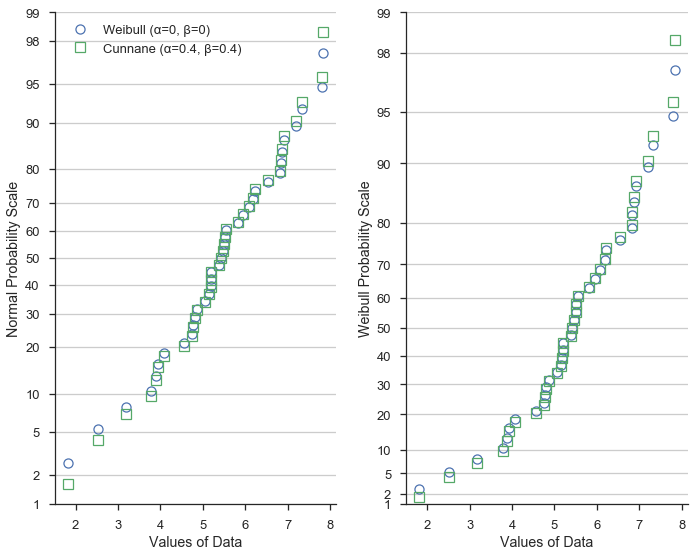
这表明绘图位置的不同公式在数据集的极端值处差异最大。
哈森绘图位置¶
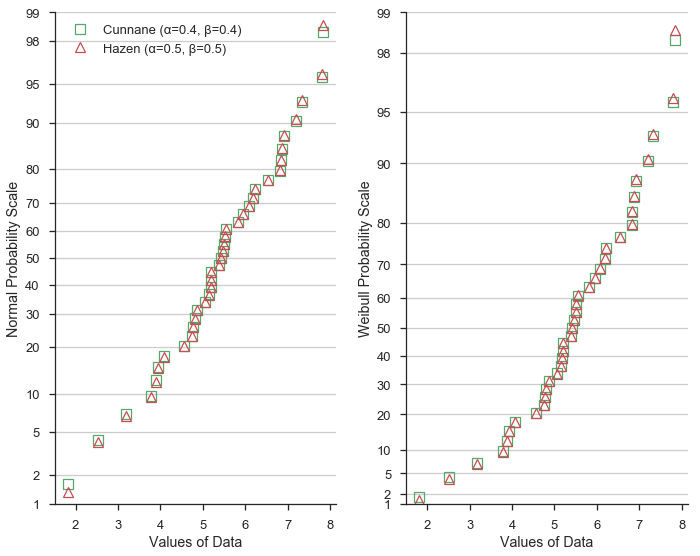
接下来,我们比较Hazen/类型5(α=0.5, β=0.5)公式与Cunnane。Hazen绘图位置(显示为红色三角形)代表数据集经验累积分布函数的分段线性插值。
鉴于α和β=0.5的值与Cunnane值仅略有不同,绘图位置可预测地相似。
h_opts = {'label': 'Hazen (α=0.5, β=0.5)', 'marker': '^', 'markeredgecolor': 'r'}
fig, (ax1, ax2) = pyplot.subplots(figsize=(10, 8), ncols=2, sharex=True, sharey=False)
for dist, ax in zip([None, weibull], [ax1, ax2]):
for opts, postype in zip([c_opts, h_opts,], ['cunnane', 'Hazen']):
probscale.probplot(data, ax=ax, dist=dist, probax='y',
scatter_kws={**opts, **common_opts},
pp_kws={'postype': postype})
format_axes(ax1, ax2)
fig.tight_layout()
总结¶
冒着显示非常杂乱且难以阅读的图形的风险,让我们将所有三者放在相同的正态概率刻度上
fig, ax1 = pyplot.subplots(figsize=(6, 8))
for opts, postype in zip([w_opts, c_opts, h_opts,], ['weibull', 'cunnane', 'hazen']):
probscale.probplot(data, ax=ax1, dist=None, probax='y',
scatter_kws={**opts, **common_opts},
pp_kws={'postype': postype})
format_axes(ax1, None)
fig.tight_layout()
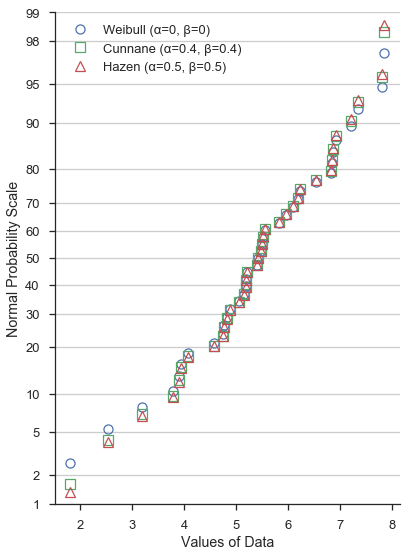
再次强调,α和β的不同值并不会显著改变概率图在——比方说——下四分位数和上四分位数之间的形状。然而,超出四分位数后,差异会更加明显。
下面的单元格计算了我们已研究的三组 α 和 β 值的绘图位置,并打印前十个值以便于比较。
# weibull plotting positions and sorted data
w_probs, _ = probscale.plot_pos(data, postype='weibull')
# normal plotting positions, returned "data" is identical to above
c_probs, _ = probscale.plot_pos(data, postype='cunnane')
# type 4 plot positions
h_probs, _ = probscale.plot_pos(data, postype='hazen')
# convert to percentages
w_probs *= 100
c_probs *= 100
h_probs *= 100
print('Weibull: ', numpy.round(w_probs[:10], 2))
print('Cunnane: ', numpy.round(c_probs[:10], 2))
print('Hazen: ', numpy.round(h_probs[:10], 2))
Weibull: [ 2.63 5.26 7.89 10.53 13.16 15.79 18.42 21.05 23.68 26.32]
Cunnane: [ 1.61 4.3 6.99 9.68 12.37 15.05 17.74 20.43 23.12 25.81]
Hazen: [ 1.35 4.05 6.76 9.46 12.16 14.86 17.57 20.27 22.97 25.68]